MathVibes

Eid Mubarak special integral Sending warm wishes to everyone celebrating Eid Mubarak! May your days be filled with joy, love, and happiness. Follow @mathvibes01 for more 🔥 #math #manim #python #mathematics

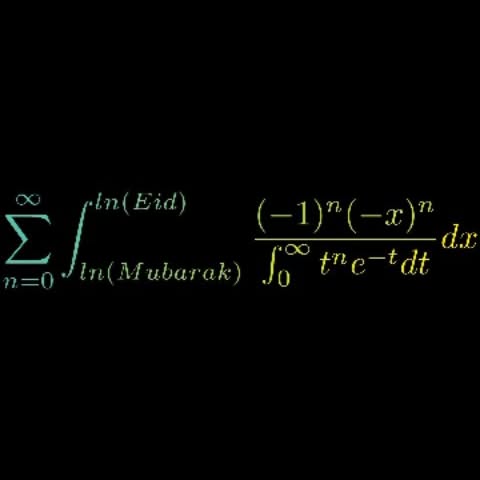
Eid Mubarak special integral Sending warm wishes to everyone celebrating Eid Mubarak! May your days be filled with joy, love, and happiness. Follow @mathvibes01 for more 🔥 #math #manim #python #mathematics

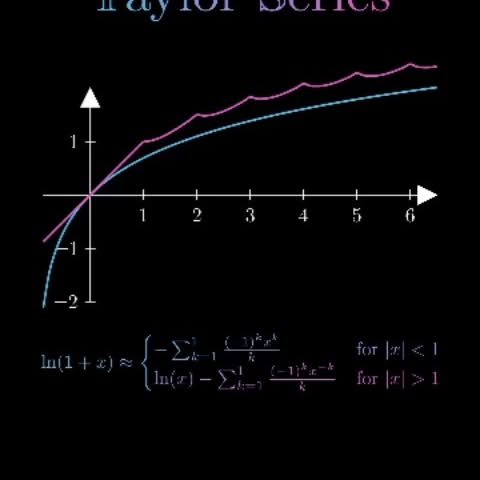
The natural logarithm of a number is its logarithm to the base of the mathematical constant e, which is an irrational and transcendental number approximately equal to 2.718281828459. The natural logarithm of x is generally written as ln x, loge x, or sometimes, if the base e is implicit, simply log x. Parentheses are sometimes added for clarity, giving ln(x), loge(x), or log(x). This is done particularly when the argument to the logarithm is not a single symbol, so as to prevent ambiguity. In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor series are equal near this point. Taylor series are named after Brook Taylor, who introduced them in 1715. A Taylor series is also called a Maclaurin series when 0 is the point where the derivatives are considered, after Colin Maclaurin, who made extensive use of this special case of Taylor series in the 18th century. Follow @mathvibes01 for more 🔥 #math #manim #python #mathematics

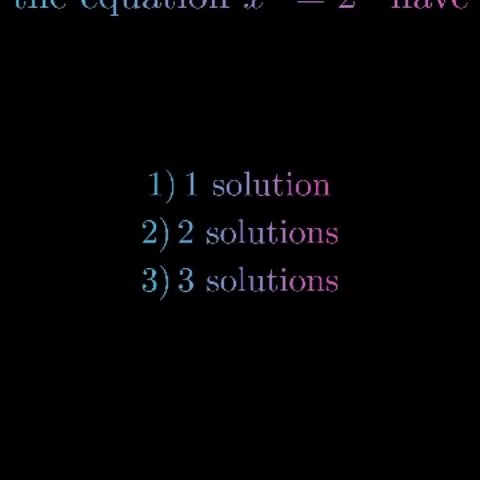
In mathematics, the exponential function is the unique real function which maps zero to one and has a derivative everywhere equal to its value. The exponential of a variable ⁠x is denoted ⁠exp(x) or ⁠eˣ, with the two notations used interchangeably. It is called exponential because its argument can be seen as an exponent to which a constant number e ≈ 2.718, the base, is raised. There are several other definitions of the exponential function, which are all equivalent although being of very different nature. The exponential function is occasionally called the natural exponential function, matching the name natural logarithm, for distinguishing it from some other functions that are also commonly called exponential functions. These functions include the functions of the form ⁠f(x) = bˣ, which is exponentiation with a fixed base ⁠b. More generally, and especially in applications, functions of the general form ⁠f(x) = abˣ are also called exponential functions. They grow or decay exponentially in that the rate that ⁠f(x) changes when ⁠x is increased is proportional to the current value of ⁠f(x) Follow @mathvibes01 for more 🔥 #math #manim #python #mathematics

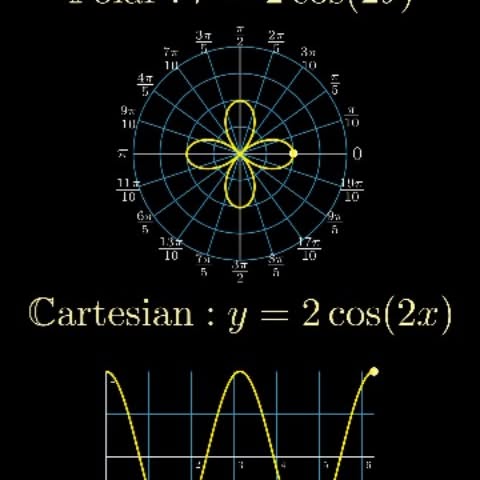
In mathematics, the polar coordinate system specifies a given point in a plane by using a distance and an angle as its two coordinates. These are the point's distance from a reference point called the pole, and the point's direction from the pole relative to the direction of the polar axis, a ray drawn from the pole. Polar coordinates are most appropriate in any context where the phenomenon being considered is inherently tied to direction and length from a center point in a plane, such as spirals. Planar physical systems with bodies moving around a central point, or phenomena originating from a central point, are often simpler and more intuitive to model using polar coordinates. Follow @mathvibes01 for more 🔥 #math #manim #python #mathematics

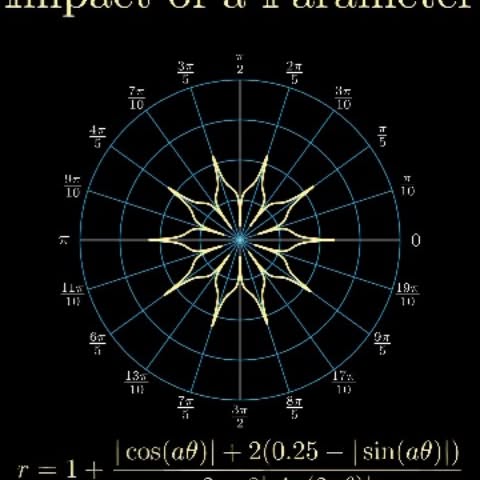
In mathematics, a parametric equation expresses several quantities, such as the coordinates of a point, as functions of one or several variables called parameters. Parametric representations are generally nonunique (see the "Examples in two dimensions" section below), so the same quantities may be expressed by a number of different parameterizations. In addition to curves and surfaces, parametric equations can describe manifolds and algebraic varieties of higher dimension, with the number of parameters being equal to the dimension of the manifold or variety, and the number of equations being equal to the dimension of the space in which the manifold or variety is considered (for curves the dimension is one and one parameter is used, for surfaces dimension two and two parameters, etc.). Parametric equations are commonly used in kinematics, where the trajectory of an object is represented by equations depending on time as the parameter. Because of this application, a single parameter is often labeled t; however, parameters can represent other physical quantities (such as geometric variables) or can be selected arbitrarily for convenience. Parameterizations are non-unique; more than one set of parametric equations can specify the same curve. Follow @mathvibes01 for more 🔥 #math #manim #python #mathematics

The Fourier transform can be formally defined as an improper Riemann integral, making it an integral transform, although this definition is not suitable for many applications requiring a more sophisticated integration theory. For example, many relatively simple applications use the Dirac delta function, which can be treated formally as if it were a function, but the justification requires a mathematically more sophisticated viewpoint. Functions that are localized in the time domain have Fourier transforms that are spread out across the frequency domain and vice versa, a phenomenon known as the uncertainty principle. The critical case for this principle is the Gaussian function, of substantial importance in probability theory and statistics as well as in the study of physical phenomena exhibiting normal distribution (e.g., diffusion). The Fourier transform of a Gaussian function is another Gaussian function. Joseph Fourier introduced sine and cosine transforms (which correspond to the imaginary and real components of the modern Fourier transform) in his study of heat transfer, where Gaussian functions appear as solutions of the heat equation. Follow @mathvibes01 & @mathswithmuza for more 🔥 #math #manim #python #mathematics

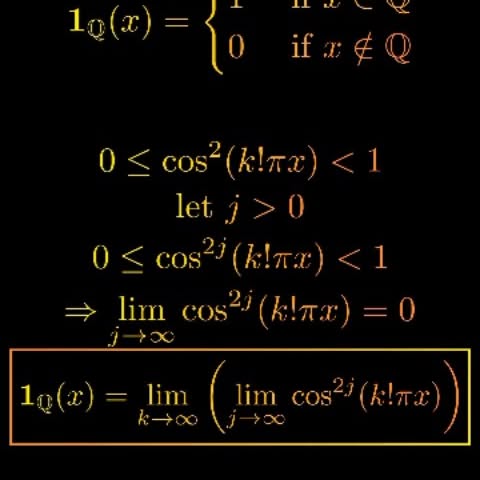
In mathematics, the Dirichlet function is the indicator function 1Q of the set of rational numbers Q, i.e. 1Q(x) = 1 if x is a rational number and 1Q(x) = 0 if x is not a rational number (i.e. is an irrational number). It is named after the mathematician Peter Gustav Lejeune Dirichlet. It is an example of a pathological function which provides counterexamples to many situations. The Dirichlet function can be constructed as the double pointwise limit of a sequence of continuous functions, as follows in the video. for integer j and k. This shows that the Dirichlet function is a Baire class 2 function. It cannot be a Baire class 1 function because a Baire class 1 function can only be discontinuous on a meagre set. Follow @mathvibes01 for more 🔥 #math #manim #python #mathematics

In mathematics, there are several integrals known as the Dirichlet integral, after the German mathematician Peter Gustav Lejeune Dirichlet, one of which is the improper integral of the sinc function over the positive real number line. It is a good illustration of special techniques for evaluating definite integrals, particularly when it is not useful to directly apply the fundamental theorem of calculus due to the lack of an elementary antiderivative for the integrand, as the sine integral, an antiderivative of the sinc function, is not an elementary function. In this case, the improper definite integral can be determined in several ways: the Laplace transform, double integration, differentiating under the integral sign, contour integration, and the Dirichlet kernel. But since the integrand is an even function, the domain of integration can be extended to the negative real number line as well. Follow @mathvibes01 for more 🔥 #math #manim #python #mathematics

In mathematics, the Fourier transform (FT) is an integral transform that takes a function as input then outputs another function that describes the extent to which various frequencies are present in the original function. The output of the transform is a complex-valued function of frequency. The term Fourier transform refers to both this complex-valued function and the mathematical operation. When a distinction needs to be made, the output of the operation is sometimes called the frequency domain representation of the original function. The Fourier transform is analogous to decomposing the sound of a musical chord into the intensities of its constituent pitches. Cristiano Ronaldo dos Santos Aveiro (born 5 February 1985) is a Portuguese professional footballer who plays as a forward for and captains both Saudi Pro League club Al-Nassr and the Portugal national team. Nicknamed CR7, he is widely regarded as one of the greatest players of all time, and has won numerous individual accolades throughout his professional footballing career, including five Ballon d'Or awards, a record three UEFA Men's Player of the Year Awards, four European Golden Shoes, and was named five times the world's best player by FIFA. He has won 34 trophies in his career, including seven league titles, five UEFA Champions Leagues and the UEFA European Championship. Ronaldo holds the records for most goals (140) and assists (42) in the Champions League, goals (14) and assists (8) in the European Championship, and most international appearances (221) and international goals (138). He is one of the few players to have made over 1,200 professional career appearances, the most by an outfield player, and has scored over 900 official senior career goals for club and country, making him the top goalscorer of all time. Follow @mathvibes01 for more 🔥 #math #manim #python #mathematics

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares on the other two sides. The theorem can be written as an equation relating the lengths of the sides a, b and the hypotenuse c, sometimes called the Pythagorean equation: a²+b²=c² The theorem is named for the Greek philosopher Pythagoras, born around 570 BC. The theorem has been proved numerous times by many different methods – possibly the most for any mathematical theorem. The proofs are diverse, including both geometric proofs and algebraic proofs, with some dating back thousands of years. When Euclidean space is represented by a Cartesian coordinate system in analytic geometry, Euclidean distance satisfies the Pythagorean relation: the squared distance between two points equals the sum of squares of the difference in each coordinate between the points. The theorem can be generalized in various ways: to higher-dimensional spaces, to spaces that are not Euclidean, to objects that are not right triangles, and to objects that are not triangles at all but n-dimensional solids. Follow @mathvibes01 for more 🔥 #math #manim #python #mathematics

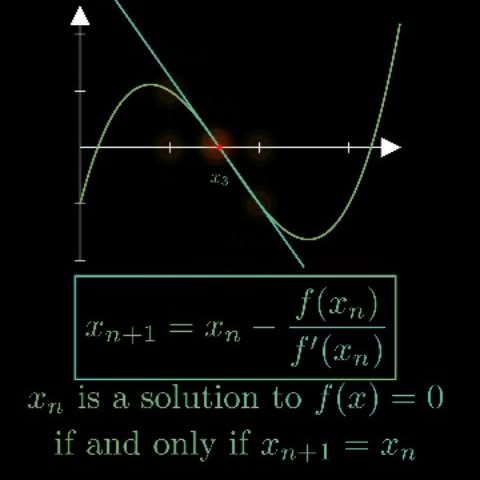
In numerical analysis, the Newton–Raphson method, also known simply as Newton's method, named after Isaac Newton and Joseph Raphson, is a root-finding algorithm which produces successively better approximations to the roots (or zeroes) of a real-valued function. The most basic version starts with a real-valued function f, its derivative f′, and an initial guess x₀ for a root of f. If f satisfies certain assumptions and the initial guess is close, then x₁ = x₀ - f(x₀)/f'(x₀) is a better approximation of the root than x₀. Geometrically, (x₁, 0) is the x-intercept of the tangent of the graph of f at (x₀, f(x₀)): that is, the improved guess, x1, is the unique root of the linear approximation of f at the initial guess, x₀. The process is repeated as xₙ₊₁ = xₙ - f(xₙ)/f'(xₙ) until a sufficiently precise value is reached. The number of correct digits roughly doubles with each step. This algorithm is first in the class of Householder's methods, and was succeeded by Halley's method. The method can also be extended to complex functions and to systems of equations. Follow @mathvibes01 for more 🔥 #math #manim #python #mathematics